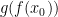Kontinuitet – Henriksen

Definition
kontinuitet, uafbrudt sammenhæng. I matematik siges en funktion at være kontinuert, hvis den ikke overspringer værdier, det vil sige at dens grafiske billede forløber ubrudt uden huller eller spring
denstoredanske.dk

En funktion $f(x)$ siges at være kontinuert i et interval $[a; b]$ , når den uden “brud” gennemløber intervallet. Hvis du kan tegne grafen uden at løfte blyantspidsen fra papiret, er den kontinuert.

Et eksempel på en kontinuert funktion kunne for eksempel være

Det ses her, at funktionen er sammenhængende i hele definitionsintervallet og derfor er den en kontinuert funktion, selv om det laver et knæk.

En funktion der ikke er kontinuert hedder en diskontinuert funktion og kunne for eksempel være

Men den kunne også godt være

Begge funktioner er defineret i hele definitionsintervallet, men begge springer når x bliver lig med -1.

De funktioner som vi har mødt indtil videre er alle kontinuerte.

Generelt vil der for funktioner gælde at

Såfremt funktionerne $f(x)$ og $g(x)$ er kontinuerte i punktet $x_0$ , da vil følgende kombinationer af $f$ og $g$ også være kontinuerte i punktet $x_0$
$f(x_0) + g(x_0)$
$f(x_0) + g(x_0)$
$f(x)\cdot g(x)$
$\frac{f(x_0)}{g(x_0)}$ , $g(x_0)\neq 0$
$f(g(x_0))$ og $g(f(x_0))$